

Next: Hollow cylinder, transient 1-D.
Up: Cylindrical Coordinates. Transient 1-D.
Previous: Infinite body with circular
R01 Solid cylinder 0 < r < b, with G = 0 (Dirichlet) at r = b.
GR01(r, t 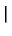 r r , ,
 ) ) |
= |
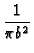 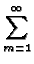 exp exp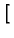 -
- 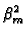 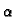 (t - (t -  )/b2 )/b2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/b^{2}}\right]$](img282.gif) |
|
| |
|
x ![$\displaystyle {\frac{J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime }/b)}{\left[
J_{1}(\beta _{m})\,\right] ^{2}}}$](img283.gif) |
|
with eigenvalues given by
J0( ) = 0.
) = 0.
R02 Solid cylinder 0 < r < b, with
 G/
G/ r = 0
(Neumann) at r = b.
r = 0
(Neumann) at r = b.
GR02(r, t 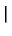 r r , ,
 ) ) |
= |
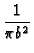 ![$\displaystyle \left[\vphantom{
1+\sum_{m=1}^{\infty }\exp \left[ -\beta _{m}^{2}\alpha (t-\tau )/b^{2}%
\right] }\right.$](img285.gif) 1 + 1 + 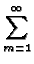 exp exp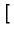 -
- 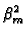 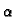 (t - (t -  )/b2 )/b2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/b^{2}%
}\right]$](img287.gif)
![$\displaystyle \left.\vphantom{
1+\sum_{m=1}^{\infty }\exp \left[ -\beta _{m}^{2}\alpha (t-\tau )/b^{2}%
\right] }\right.$](img288.gif) |
|
| |
|
![$\displaystyle \left.\vphantom{ \times \frac{J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime }/b)}{%
\left[ J_{0}(\beta _{m})\,\right] ^{2}}}\right.$](img289.gif) x
x ![$\displaystyle {\frac{J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime }/b)}{%
\left[ J_{0}(\beta _{m})\,\right] ^{2}}}$](img290.gif)
![$\displaystyle \left.\vphantom{ \times \frac{J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime }/b)}{%
\left[ J_{0}(\beta _{m})\,\right] ^{2}}}\right]$](img291.gif) |
|
with eigenvalues given by
J1( ) = 0.
) = 0.
R03 Solid cylinder 0 < r < b, with
k G/
G/ r + hG = 0 (convection) at r = b.
r + hG = 0 (convection) at r = b.
GR03(r, t 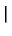 r r , ,
 ) ) |
= |
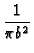 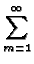 exp exp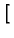 -
- 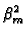 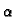 (t - (t -  )/b2 )/b2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/b^{2}}\right]$](img282.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime
}/b)}{\left[ J_{0}(\beta _{m})\,\right] ^{2}(B^{2}+\beta _{m}^{2})}}$](img292.gif) |
|
with eigenvalues given by -
 J1(
J1( ) + BJ0(
) + BJ0( ) = 0
, and B = hb/k.
) = 0
, and B = hb/k.


Next: Hollow cylinder, transient 1-D.
Up: Cylindrical Coordinates. Transient 1-D.
Previous: Infinite body with circular
Kevin D. Cole
2002-12-31
![$\displaystyle {\frac{J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime }/b)}{\left[
J_{1}(\beta _{m})\,\right] ^{2}}}$](img283.gif)
![$\displaystyle {\frac{J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime }/b)}{\left[
J_{1}(\beta _{m})\,\right] ^{2}}}$](img283.gif)
![]() G/
G/![]() r = 0
(Neumann) at r = b.
r = 0
(Neumann) at r = b.
![$\displaystyle {\frac{J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime }/b)}{%
\left[ J_{0}(\beta _{m})\,\right] ^{2}}}$](img290.gif)
![]() G/
G/![]() r + hG = 0 (convection) at r = b.
r + hG = 0 (convection) at r = b.
![$\displaystyle {\frac{\beta _{m}^{2}J_{0}(\beta _{m}r/b)\,J_{0}(\beta _{m}r^{\prime
}/b)}{\left[ J_{0}(\beta _{m})\,\right] ^{2}(B^{2}+\beta _{m}^{2})}}$](img292.gif)