

Next: Radial-spherical coordinates. Transient 1-D.
Up: Cylindrical Coordinates. Transient 1-D.
Previous: Solid cylinder transient 1-D.
R11 Hollow cylinder a < r < b, with G = 0 (Dirichlet) at r = a and r = b.
GR11(r, t 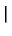 r r , ,
 ) ) |
= |
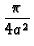 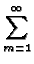 exp exp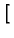 -
- 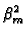 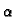 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}\,\left[ J_{0}(\beta _{m})\,\right]
^{2}R(r)...
...ft[ J_{0}(\beta _{m})\,\right] ^{2}-\left[
J_{0}(\beta _{m}b/a)\,\right] ^{2}}}$](img296.gif) |
|
| where R(r) |
= |
J0( 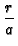 )Y0( )Y0(  ) - Y0( ) - Y0( 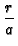 )J0( )J0(  ) ) |
|
with eigenvalues given by
J0( )Y0(
)Y0( b/a) - Y0(
b/a) - Y0( )J0(
)J0( b/a) = 0.
b/a) = 0.
R12 Hollow cylinder a < r < b, with G = 0 (Dirichlet) at r = a and
 G/
G/ r = 0 (Neumann)at r = b.
r = 0 (Neumann)at r = b.
GR12(r, t 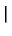 r r , ,
 ) ) |
= |
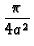 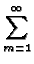 exp exp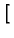 -
- 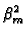 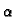 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{0}(\beta _{m})\,\right] ^{2}}{\left[
J_{0}(\beta _{m})\,\right] ^{2}-\left[ J_{1}(\beta _{m}b/a)\,\right] ^{2}}}$](img299.gif) R(r) R(r R(r) R(r ) ) |
|
| where R(r) |
= |
J0( 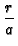 )Y1( )Y1(  ) - Y0( ) - Y0( 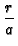 )J1( )J1(  ) ) |
|
with eigenvalues given by
J0( )Y1(
)Y1( b/a) - Y0(
b/a) - Y0( )J1(
)J1( b/a) = 0.
b/a) = 0.
R13 Hollow cylinder a < r < b, with G = 0 (Dirichlet) at r = a and
k G/
G/ r + hG = 0 (convection) at r = b.
r + hG = 0 (convection) at r = b.
GR13(r, t 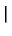 r r , ,
 ) ) |
= |
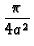 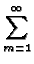 exp exp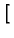 -
- 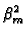 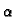 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{0}(\beta _{m})\,\right] ^{2}}{%
(B^{2}+\beta _{m}^{2})\left[ J_{0}(\beta _{m})\,\right] ^{2}-V_{0}{}^{2}}}$](img300.gif) R(r) R(r R(r) R(r ) ) |
|
| where R(r) |
= |
S0J0( 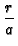 ) - V0Y0( ) - V0Y0( 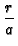 ) ) |
|
| with V0 |
= |
- J1( J1(  ) + BJ0( ) + BJ0(  ) ) |
|
| S0 |
= |
-  Y1( Y1(  ) + BY0( ) + BY0(  ) ) |
|
| B |
= |
ha/k |
|
Eigenvalues are given by
S0J0( ) - V0Y0(
) - V0Y0( ) = 0
.
) = 0
.
R21 Hollow cylinder a < r < b, with
 G/
G/ r = 0 (Dirichlet) at r = a and G = 0 (Neumann) at r = b.
r = 0 (Dirichlet) at r = a and G = 0 (Neumann) at r = b.
GR21(r, t 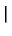 r r , ,
 ) ) |
= |
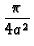 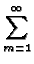 exp exp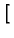 -
- 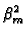 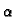 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{1}(\beta _{m})\,\right] ^{2}}{\left[
J_{1}(\beta _{m})\,\right] ^{2}-\left[ J_{0}(\beta _{m}b/a)\,\right] ^{2}}}$](img301.gif) R(r) R(r R(r) R(r ) ) |
|
| where R(r) |
= |
J0( 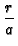 )Y0( )Y0(  ) - Y0( ) - Y0( 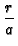 )J0( )J0(  ) ) |
|
with eigenvalues given by
J1( )Y0(
)Y0( b/a) - Y1(
b/a) - Y1( )J0(
)J0( b/a) = 0.
b/a) = 0.
R22 Hollow cylinder a < r < b, with
 G/
G/ r = 0 (Dirichlet) at r = a and G = 0 (Neumann) at r = b.
r = 0 (Dirichlet) at r = a and G = 0 (Neumann) at r = b.
GR22(r, t 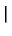 r r , ,
 ) ) |
= |
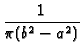 +
+ 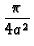 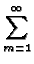 exp exp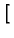 -
- 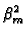 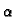 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{1}(\beta _{m})\,\right] ^{2}}{\left[
J_{1}(\beta _{m})\,\right] ^{2}-\left[ J_{1}(\beta _{m}b/a)\,\right] ^{2}}}$](img303.gif) R(r) R(r R(r) R(r ) ) |
|
| where R(r) |
= |
J0( 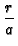 )Y1( )Y1(  ) - Y0( ) - Y0( 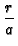 )J1( )J1(  ) ) |
|
with eigenvalues given by
J1( )Y1(
)Y1( b/a) - Y1(
b/a) - Y1( )J1(
)J1( b/a) = 0.
b/a) = 0.
R23 Hollow cylinder a < r < b, with
 G/
G/ r = 0 (Neumann) at r = a and
k
r = 0 (Neumann) at r = a and
k G/
G/ r + hG = 0 (convection) at r = b.
r + hG = 0 (convection) at r = b.
GR23(r, t 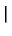 r r , ,
 ) ) |
= |
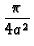 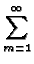 exp exp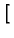 -
- 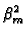 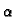 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{1}(\beta _{m})\,\right] ^{2}}{%
(B^{2}+\beta _{m}^{2})\left[ J_{1}(\beta _{m})\,\right] ^{2}-V_{0}{}^{2}}}$](img304.gif) R(r) R(r R(r) R(r ) ) |
|
| where R(r) |
= |
S0J0( 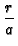 ) - V0Y0( ) - V0Y0( 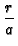 ) ) |
|
| with V0 |
= |
- J1( J1(  ) + BJ0( ) + BJ0(  ) ) |
|
| S0 |
= |
-  Y1( Y1(  ) + BY0( ) + BY0(  ) ) |
|
| B |
= |
ha/k |
|
Eigenvalues are given by
S0J1( ) - V0Y1(
) - V0Y1( ) = 0
.
) = 0
.
R31 Hollow cylinder a < r < b, with
- k G/
G/ r + hG = 0 (convection) at r = a and G = 0 (Dirichlet) at r = b.
r + hG = 0 (convection) at r = a and G = 0 (Dirichlet) at r = b.
GR31(r, t 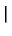 r r , ,
 ) ) |
= |
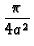 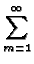 exp exp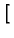 -
- 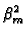 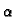 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}U_{0}^{2}}{U_{0}^{2}-(B^{2}+\beta _{m}^{2})%
\left[ J_{0}(\beta _{m}b/a)\,\right] ^{2}}}$](img305.gif) R(r) R(r R(r) R(r ) ) |
|
| where R(r) |
= |
J0( 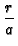 )Y0( )Y0(  ) - Y0( ) - Y0( 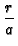 )J0( )J0(  ) ) |
|
| with U0 |
= |
-  J1( J1( ) + BJ0( ) + BJ0( ) ) |
|
| W0 |
= |
-  Y1( Y1( ) + BY0( ) + BY0( ) ) |
|
| B |
= |
ha/k |
|
Eigenvalues are given by
U0Y0( b/a) - W0J0(
b/a) - W0J0( b/a) = 0.
b/a) = 0.
R32 Hollow cylinder a < r < b, with
- k G/
G/ r + hG = 0 (convection) at r = a and
r + hG = 0 (convection) at r = a and
 G/
G/ r = 0 (Neumann) at r = b.
r = 0 (Neumann) at r = b.
GR32(r, t 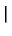 r r , ,
 ) ) |
= |
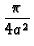 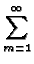 exp exp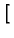 -
- 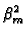 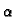 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x ![$\displaystyle {\frac{\beta _{m}^{2}U_{0}^{2}}{U_{0}^{2}-(B^{2}+\beta _{m}^{2})%
\left[ J_{1}(\beta _{m}b/a)\,\right] ^{2}}}$](img306.gif) R(r) R(r R(r) R(r ) ) |
|
| where R(r) |
= |
J0( 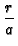 )Y1( )Y1(  ) - Y0( ) - Y0( 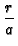 )J1( )J1(  ) ) |
|
| with U0 |
= |
-  J1( J1( ) + BJ0( ) + BJ0( ) ) |
|
| W0 |
= |
-  Y1( Y1( ) + BY0( ) + BY0( ) ) |
|
| B |
= |
ha/k |
|
Eigenvalues are given by
U0Y1( b/a) - W0J1(
b/a) - W0J1( b/a) = 0.
b/a) = 0.
R33 Hollow cylinder a < r < b, with
- k G/
G/ r + h1G = 0 (convection) at r = a and
k
r + h1G = 0 (convection) at r = a and
k G/
G/ r + h2G = 0
(convection) at r = b.
r + h2G = 0
(convection) at r = b.
GR33(r, t 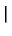 r r , ,
 ) ) |
= |
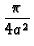 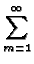 exp exp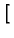 -
- 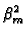 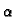 (t - (t -  )/a2 )/a2![$\displaystyle \left.\vphantom{ -\beta _{m}^{2}\alpha (t-\tau )/a^{2}}\right]$](img295.gif) |
|
| |
|
x 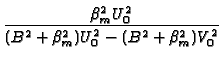 R(r) R(r R(r) R(r ) ) |
|
| where R(r) |
= |
S0J0( 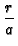 ) - V0Y0( ) - V0Y0( 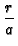 ) ) |
|
| with S0 |
= |
-  Y1( Y1(  ) + B2Y0( ) + B2Y0(  ) ) |
|
| with U0 |
= |
-  J1( J1( ) - B1J0( ) - B1J0( ) ) |
|
| V0 |
= |
-  J1( J1(  ) + B2J0( ) + B2J0( 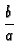 ) ) |
|
| W0 |
= |
-  Y1( Y1( ) + B1Y0( ) + B1Y0( ) ) |
|
| B1 |
= |
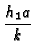 ; B2 = ; B2 = 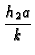 |
|
Eigenvalues are given by
S0U0 - V0W0 = 0.


Next: Radial-spherical coordinates. Transient 1-D.
Up: Cylindrical Coordinates. Transient 1-D.
Previous: Solid cylinder transient 1-D.
Kevin D. Cole
2002-12-31
![$\displaystyle {\frac{\beta _{m}^{2}\,\left[ J_{0}(\beta _{m})\,\right]
^{2}R(r)...
...ft[ J_{0}(\beta _{m})\,\right] ^{2}-\left[
J_{0}(\beta _{m}b/a)\,\right] ^{2}}}$](img296.gif)
![$\displaystyle {\frac{\beta _{m}^{2}\,\left[ J_{0}(\beta _{m})\,\right]
^{2}R(r)...
...ft[ J_{0}(\beta _{m})\,\right] ^{2}-\left[
J_{0}(\beta _{m}b/a)\,\right] ^{2}}}$](img296.gif)
![]() G/
G/![]() r = 0 (Neumann)at r = b.
r = 0 (Neumann)at r = b.
![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{0}(\beta _{m})\,\right] ^{2}}{\left[
J_{0}(\beta _{m})\,\right] ^{2}-\left[ J_{1}(\beta _{m}b/a)\,\right] ^{2}}}$](img299.gif) R(r) R(r
R(r) R(r![]() G/
G/![]() r + hG = 0 (convection) at r = b.
r + hG = 0 (convection) at r = b.
![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{0}(\beta _{m})\,\right] ^{2}}{%
(B^{2}+\beta _{m}^{2})\left[ J_{0}(\beta _{m})\,\right] ^{2}-V_{0}{}^{2}}}$](img300.gif) R(r) R(r
R(r) R(r![]() G/
G/![]() r = 0 (Dirichlet) at r = a and G = 0 (Neumann) at r = b.
r = 0 (Dirichlet) at r = a and G = 0 (Neumann) at r = b.
![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{1}(\beta _{m})\,\right] ^{2}}{\left[
J_{1}(\beta _{m})\,\right] ^{2}-\left[ J_{0}(\beta _{m}b/a)\,\right] ^{2}}}$](img301.gif) R(r) R(r
R(r) R(r![]() G/
G/![]() r = 0 (Dirichlet) at r = a and G = 0 (Neumann) at r = b.
r = 0 (Dirichlet) at r = a and G = 0 (Neumann) at r = b.
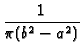 +
+ ![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{1}(\beta _{m})\,\right] ^{2}}{\left[
J_{1}(\beta _{m})\,\right] ^{2}-\left[ J_{1}(\beta _{m}b/a)\,\right] ^{2}}}$](img303.gif) R(r) R(r
R(r) R(r![]() G/
G/![]() r = 0 (Neumann) at r = a and
k
r = 0 (Neumann) at r = a and
k![]() G/
G/![]() r + hG = 0 (convection) at r = b.
r + hG = 0 (convection) at r = b.
![$\displaystyle {\frac{\beta _{m}^{2}\left[ J_{1}(\beta _{m})\,\right] ^{2}}{%
(B^{2}+\beta _{m}^{2})\left[ J_{1}(\beta _{m})\,\right] ^{2}-V_{0}{}^{2}}}$](img304.gif) R(r) R(r
R(r) R(r![]() G/
G/![]() r + hG = 0 (convection) at r = a and G = 0 (Dirichlet) at r = b.
r + hG = 0 (convection) at r = a and G = 0 (Dirichlet) at r = b.
![$\displaystyle {\frac{\beta _{m}^{2}U_{0}^{2}}{U_{0}^{2}-(B^{2}+\beta _{m}^{2})%
\left[ J_{0}(\beta _{m}b/a)\,\right] ^{2}}}$](img305.gif) R(r) R(r
R(r) R(r![]() G/
G/![]() r + hG = 0 (convection) at r = a and
r + hG = 0 (convection) at r = a and
![]() G/
G/![]() r = 0 (Neumann) at r = b.
r = 0 (Neumann) at r = b.
![$\displaystyle {\frac{\beta _{m}^{2}U_{0}^{2}}{U_{0}^{2}-(B^{2}+\beta _{m}^{2})%
\left[ J_{1}(\beta _{m}b/a)\,\right] ^{2}}}$](img306.gif) R(r) R(r
R(r) R(r![]() G/
G/![]() r + h1G = 0 (convection) at r = a and
k
r + h1G = 0 (convection) at r = a and
k![]() G/
G/![]() r + h2G = 0
(convection) at r = b.
r + h2G = 0
(convection) at r = b.
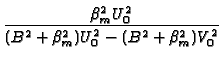 R(r) R(r
R(r) R(r