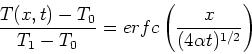

Next: 1D Slab heated at
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: 1D infinite body with
Consider the temperature in semi-infinite body with a specified temperature
applied to the 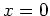 boundary. The temperature satisfies the following equations:
boundary. The temperature satisfies the following equations:
The above problem has two non-homogeneous terms, however one may be
eliminated to simplify the problem by normalizing the temperature.
Let
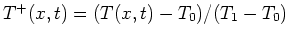 . If you replace
. If you replace 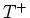 into the above problem, the initial condition is zero and the
boundary temperature is unity. Then this example is described by
number X10B1T0. The temperature is given
by the type 1 boundary term of the GF solution equation, as follows:
into the above problem, the initial condition is zero and the
boundary temperature is unity. Then this example is described by
number X10B1T0. The temperature is given
by the type 1 boundary term of the GF solution equation, as follows:
![\begin{displaymath}
\frac{T(x,t)-T_0}{T_1 - T_0} = \alpha \int_{\tau=0}^t
\left...
...al G_{X10}}{\partial x^{\prime}} \right]_{x^{\prime}=0} d \tau
\end{displaymath}](img89.png) |
(9) |
Note that here the sign of the derivative has been chosen by the outward normal
according to
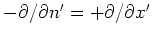 .
The GF is given by
.
The GF is given by
![\begin{displaymath}
G_{X10}(x,t \mid x^{\prime},\tau ) =[4 \pi \alpha (t-\tau)]^...
...-\frac{(x+x^{\prime })^{2}}{4 \alpha (t-\tau)}\right] \right\}
\end{displaymath}](img91.png) |
(10) |
The required derivative of the GF with respect to 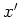 evaluated at
evaluated at
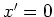 is given by
is given by
![\begin{displaymath}
\left[ \frac{\partial G_{X10}}{\partial x^{\prime}} \right]_...
...]^{3/2} }
\exp \left[ \frac{-x^{2}}{4 \alpha (t-\tau)}\right]
\end{displaymath}](img94.png) |
(11) |
Replace the above GF derivative into the GF solution equation to find
the temperature; the integral may be evaluated as an error function.
![\begin{displaymath}
\frac{T(x,t)-T_0}{T_1 - T_0} = \left[ 1- erf \left( \frac{x}{(4 \alpha t)^{1/2}} \right) \right ]
\end{displaymath}](img95.png) |
(12) |
or as the complementary error function
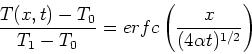 |
(13) |
Alternately, this problem could have been solved as an initial condition problem
if the temperature were normalized as
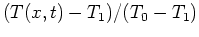 .
.

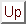

Next: 1D Slab heated at
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: 1D infinite body with
2004-01-31
![]() boundary. The temperature satisfies the following equations:
boundary. The temperature satisfies the following equations:
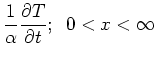
![\begin{displaymath}
\frac{T(x,t)-T_0}{T_1 - T_0} = \alpha \int_{\tau=0}^t
\left...
...al G_{X10}}{\partial x^{\prime}} \right]_{x^{\prime}=0} d \tau
\end{displaymath}](img89.png)
![\begin{displaymath}
G_{X10}(x,t \mid x^{\prime},\tau ) =[4 \pi \alpha (t-\tau)]^...
...-\frac{(x+x^{\prime })^{2}}{4 \alpha (t-\tau)}\right] \right\}
\end{displaymath}](img91.png)
![]() evaluated at
evaluated at
![]() is given by
is given by
![\begin{displaymath}
\left[ \frac{\partial G_{X10}}{\partial x^{\prime}} \right]_...
...]^{3/2} }
\exp \left[ \frac{-x^{2}}{4 \alpha (t-\tau)}\right]
\end{displaymath}](img94.png)
![\begin{displaymath}
\frac{T(x,t)-T_0}{T_1 - T_0} = \left[ 1- erf \left( \frac{x}{(4 \alpha t)^{1/2}} \right) \right ]
\end{displaymath}](img95.png)