

Next: Solid cylinder with internal
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: Semi-infinite body heated at
The temperature in a 1D slab with a short-duration
heat flux on one face and with a fixed
temperature on the other face is discussed in this example. The
initial temperature is zero and there is no internal heat generation.
The boundary value problem for this case is given by:
This example is case X21B(t5)0T0. The method of GF is well
suited to piecewise continuous heating. The temperature is found
from the ``type 2'' boundary term of the GF solution equation
with the heat flux substituted in the form 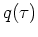 :
:
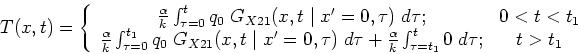 |
(15) |
The integral for 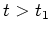 has been written in two pieces to emphasize
the piecewise heating function. There are two forms of the GF
for this geometry, and the one used here is best for large
values of
has been written in two pieces to emphasize
the piecewise heating function. There are two forms of the GF
for this geometry, and the one used here is best for large
values of 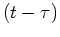 . The large-time GF is given by
. The large-time GF is given by
The time integral in the GF solution may be distributed over the series
term by term, and the integral falls only on the exponential portion of
each term. When the GF is substituted into the temperature expression and
evaluated, the result is:
Although the temperature is caused by a discontinous heating history, the
temperature is continous and smoothly varying in space and time.
At large time the introduced heat leaves the body and the steady-state
temperature is zero.


Next: Solid cylinder with internal
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: Semi-infinite body heated at
2004-01-31

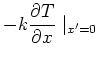


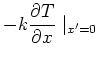

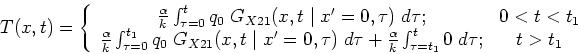
![$\displaystyle \frac{2}{L}%
\sum_{m=1}^{\infty }\exp \left[ -\frac{\beta _{m}^{2...
...2}}%
\right] \cos (\beta _{m}\frac{x}{L})\cos (\beta _{m}\frac{x^{\prime }}{L})$](img108.png)
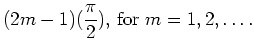
![$\displaystyle 2\frac{q_0L}{k} \sum_{m=1}^\infty \cos(\beta_m x/L)
\frac{1}{\beta_m^2}
[1- e^{-\beta_m^2 \alpha t/L^2}]$](img112.png)
![$\displaystyle 2\frac{q_0L}{k} \sum_{m=1}^\infty \cos(\beta_m x/L)
\frac{1}{\beta_m^2}
[e^{-\beta_m^2 \alpha (t-t_1)/L^2}- e^{-\beta_m^2 \alpha t/L^2}]$](img114.png)