K(w) = 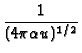 e-w2/(4 e-w2/(4 |
(1) |
| Table | Contents |
| 1A | Small-Time GF |
| 1B | Small-Time GF, compact form |
| 2A | Boundary GF evaluated at n' = 0 |
| 2B | Derivatives of boundary GF evaluated at n' = 0 |
| 3A | Boundary GF evaluated at n' = L |
| 3B | Derivative of boundary GF evaluated at n' = L |
| 4A | Integrals of GF w.r.t. x |
| 4B | Derivative w.r.t. x of integrals of GF |
Notation used in tables.
Fundamental heat conduction solution:
K(w) = 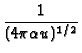 e-w2/(4 e-w2/(4 |
(1) |
| Hi(w) = exp |
(2) |
| E(w) = erfc |
(3) |
Table 1A. Small time Green's functions. The GX00, GX10, GX20 and GX30 cases
are exact. The other cases include up to two reflections. The expressions for single
reflections are obtained by dropping the terms which are function of either 2L - x + x' or 2L + x - x.
Expressions for the y-direction are found by replacing x by y, x' by y' and L by W.
Similar results are obtained for the z-direction
by using z, z' and H.
| Number | Equation |
1A.X00 |
GX10(x, x', u) = K(x - x') |
1A.X10 |
GX10(x, x', u) = K(x - x') - K(x + x') |
1A.X11 |
GX11(x, x', u) |
| + K(2L - x + x') + K(2L + x - x') | |
1A.X12 |
GX12(x, x', u) |
| - K(2L - x + x') - K(2L + x - x') | |
1A.X13 |
GX13(x, x', u) |
| - K(2L - x + x') - K(2L + x - x') - (hL/k)HL(2L - x - x') | |
| + (hL/k)HL(2L - x + x') + (hL/k)HL(2L + x - x') | |
1A.X20 |
GX20(x, x', u) = K(x - x') + K(x + x') |
1A.X21 |
GX21(x, x', u) |
| - K(2L - x + x') - K(2L + x - x') | |
1A.X22 |
GX22(x, x', u) |
| + K(2L - x + x') + K(2L + x - x') | |
1A.X23 |
GX23(x, x', u) |
| - (hL/k)HL(2L - x - x') + K(2L - x + x') + K(2L + x - x') | |
| - (hL/k)HL(2L - x + x') - (hL/k)HL(2L + x - x') | |
1A.X30 |
GX30(x, x', u) = K(x - x') + K(x + x') - (h0/k)H0(x + x') |
1A.X31 |
GX31(x, x', u) |
| - K(2L - x - x') - K(2L - x + x') - K(2L + x - x') | |
| + (h0/k)H0(2L - x + x') + (h0/k)H0(2L + x - x') | |
1A.X32 |
GX32(x, x', u) |
| + K(2L - x - x') + K(2L - x + x') + K(2L + x - x') | |
| - (h0/k)H0(2L - x + x') - (h0/k)H0(2L + x - x') | |
1A.X33a |
GX33(x, x', u) |
| K(2L - x - x') - (hL/k)HL(2L - x - x') + K(2L - x + x') | |
| + K(2L + x - x') - (h0/k)H0(2L - x + x') | |
| - (h0/k)H0(2L + x - x') - (hL/k)HL(2L - x + x') | |
| - (hL/k)HL(2L + x - x') + JH(L, x, x') | |
|
where for h0 |
|
1A.X33b |
JH(L, x, x') = (2h0hL/(k(hL - h0)))[H0(2L - x + x') |
| + H0(2L + x - x') - HL(2L - x + x') - HL(2L + x - x')], | |
| and for h0 = hL | |
1A.X33c |
JH(L, x, x') = (2h02/k2){4 |
|
- (2L - x + x' + 2(h0/k) |
|
|
- (2L + x - x' + 2(h0/k) |
Table 1B. Small time Green's functions in compact form.
| Number | Equation |
1B.X10 |
GX10(x, x', u) = K(x - x') - K(x + x') |
| 1B.X11 |
GX11(x, x', u) |
|
|
|
1B.X12 |
GX12(x, x', u) |
1B.X13 |
GX13(x, x', u) |
|
|
|
| - HL(2L + x - x')] | |
1B.X20 |
GX20(x, x', u) = K(x - x') + K(x + x') |
1B.X21 |
GX21(x, x', u) |
|
|
|
1B.X22 |
GX22(x, x', u) |
1B.X23 |
GX23(x, x', u) |
|
|
|
| + HL(2L + x - x')] | |
1B.X31 |
GX31(x, x', u) |
|
|
|
1B.X32 |
GX32(x, x', u) |
|
|
|
1B.X33 |
GX33(x, x', u) |
| (see Table 1A, entry X33, for JH) |
Table 2A. Boundary Green's functions for boundary conditions of the 2nd and 3rd
kinds and
negative of the derivative of the Green's function (with respect to the outward pointing normal)
for the 1st kind of boundary condition. Evaluated at x' = 0.
(Notice for this boundary n' = x'.)
Simpler and still accurate equations are given if the functions of 2L + x are dropped.
| Number | Equation |
| 2A.X10 |
- |
2A.X11 |
- |
|
-2(2L - x)K(2L - x) + (2L + x)K(2L + x)], x |
|
2A.X12 |
- |
|
2(2L - x)K(2L - x) - (2L + x)K(2L + x)], x |
|
2A.X13 |
- |
| - (2L + x)K(2L + x)] + 2(hL/k)2HL(2L - x) - (4hL/k)K(2L - x) | |
|
- (hL/k)2HL(2L + x) + (2hL/k)K(2L + x), x |
|
2A.X20 |
GX20(x, 0, u) = 2K(x) |
2A.X21 |
GX21(x, 0, u) |
2A.X22 |
GX22(x, 0, u) |
2A.X23 |
GX23(x, 0, u) |
| -2(hL/k)HL(2L - x) - (hL/k)HL(2L + x) | |
2A.X30 |
GX30(x, 0, u) = 2K(x) - (h0/k)H0(x) |
2A.X31 |
GX31(x, 0, u) |
| - (h0/k)H0(x) + (h0/k)H0(2L - x) + (h0/k)H0(2L + x) | |
2A.X32 |
GX32(x, 0, u) |
| - (h0/k)H0(x) - (h0/k)H0(2L - x) - (h0/k)H0(2L + x) | |
2A.X33a |
GX33(x, 0, u) |
| - (h0/k)H0(x) - (h0/k)H0(2L - x) - 2(hL/k)HL(2L - x) | |
| - (h0/k)H0(2L + x) - (hL/k)HL(2L + x) + JH(L, x, 0) | |
| where for
h0 |
|
2A.X33b |
JH(L, x, 0) = (2h0hL/(k(hL - h0)))[H0(2L - x) + H0(2L + x) |
| - HL(2L - x) - HL(2L + x)] | |
| and for h0 = hL, | |
2A.X33b |
JH(L, x, 0) = (2h02/k2){2( |
|
+ exp[- (2L + x)2/(4 |
|
|
- [2L + x + 2(h0/k) |
Table 2B. Derivative wrt x of Green's functions for boundary conditions of the
2nd and 3rd kinds
and negative of mixed second partial derivative wrt x and n' of the Green's function
for the 1st
kind of boundary condition. Small time forms. All evaluated at n' = 0. Simpler and still
accurate equations are given if the functions of 2L + x and 3L - x are dropped.
| Number | Equation |
| 2B.X10 |
- |
2B.X11 |
- |
|
+ K(2L - x)(1 - (2L - x)2(2 |
|
2B.X12 |
- |
|
- K(2L - x)(1 - (2L - x)2(2 |
|
2B.X13 |
- |
|
- K(2L - x)(1 - (2L - x)2(2 |
|
|
- (2L - x)(2 |
|
| -2(hL/k)3HL(2L - x) - (hL/k)3HL(2L + x) | |
2B.X20 |
|
2B.X21 |
|
| - (1/2)(2L + x)K(2L + x)] | |
2B.X22 |
|
| + (1/2)(2L + x)K(2L + x)] | |
2B.X23 |
|
| + (1/2)(2L + x)K(2L + x)] - 4(hL/k)K(2L - x) + 2(hL/k)2HL(2L - x) | |
| +2(hL/k)K(2L + x) - (hL/k)2HL(2L + x) | |
2B.X30 |
|
2B.X31 |
|
| - (1/2)(2L + x)K(2L + x)] + 2(h0/k)[K(x) + K(2L - x) | |
| - K(2L + x)] - (h0/k)2[H0(x) + H0(2L - x) - H0(2L + x)] | |
2B.X32 |
|
| + (1/2)(2L + x)K(2L + x)] + 2(h0/k)[K(x) - K(2L - x) + K(2L + x)] | |
| - (h0/k)2[H0(x) - H0(2L - x) + H0(2L + x)] | |
2B.X33a |
|
| - (2L - x)K(2L - x) + (1/2)(2L + x)K(2L + x)] + 2(h0/k)[K(x) | |
| - K(2L - x) + K(2L + x)] - (h0/k)2[H0(x) - H0(2L - x) | |
| + H0(2L + x)] - 4(hL/k)K(2L - x) + 2(hL/k)K(2L + x) | |
| + (hL/k)2[2HL(2L - x) - HL(2L + x)] + DJH(L, x, 0) | |
| where for
h0 |
|
| 2B.X33b | DJH(L, x, 0) = (2h0hL/(k(hL - h0)))[- (h0/k)(H0(2L - x) |
| - H0(2L + x)) + (hL/k)(HL(2L - x) - HL(2L + x)] | |
| and for h0 = hL, | |
2B.X33c |
JH(L, x, 0) = (2h02/k2){4(h0/k) |
|
+ [1 + (h0/k)(2L - x) + 2(h0/k)2 |
|
|
- [1 + (h0/k)(2L + x) + 2(h0/k)2 |
Table 3A. Boundary Green's functions for boundary conditions of the 2nd and 3rd
kinds and
negative of the derivative of the Green's function with respect to n' for the 1st kind of
boundary condition. Small time forms and evaluated at
n' = x' = L.
| Number | Equation |
| 3A.X11 |
- |
|
-2(L + x)K(L + x) + (3L - x)K(3L - x)], x |
|
3A.X12 |
GX12(x, L, u) |
3A.X13 |
GX13(x, L, u) |
| - (hL/k)HL(L - x) + (hL/k)HL(L + x) + (hL/k)HL(3L - x) | |
3A.X21 |
- |
|
+2(L + x)K(L + x) - (3L - x)K(3L - x)], x |
|
| 3A.X22 |
GX22(x, L, u) |
3A.X23 |
GX23(x, L, u) |
| - (hL/k)[HL(L - x) + HL(L + x) + HL(3L - x)] | |
3A.X31 |
- |
| +2(L + x)K(L + x) - (3L - x)K(3L - x)] - 4(h0/k)K(L + x) | |
| +2(h0/k)2H0(L + x) + 2(h0/k)K(3L - x) | |
|
- (h0/k)2H0(3L - x), x |
|
3A.X32 |
GX32(x, L, u) |
| -2(h0/k)H0(L + x) - (h0/k)H0(3L - x) | |
3A.X33a |
GX33(x, L, u) |
| -2(h0/k)H0(L + x) - (h0/k)H0(3L - x) - (hL/k)HL(L - x) | |
| - (hL/k)HL(L + x) - (hL/k)HL(3L - x) + JH(L, x, L) | |
| where for
h0 |
|
3A.X33b |
JH(L, x, L) |
| - HL(3L - x) - HL(L + x)] | |
| and for h0 = hL, | |
3A.X33c |
JH(L, x, x') |
|
- (3L - x + 2(h0/k) |
|
|
- (L + x + 2(h0/k) |
Table 3B. Derivative wrt x of Green's functions for Boundary Conditions
of the 2nd and 3rd Kinds
and Negative of Mixed Second Partial Derivative wrt x and n' of the Green's
function for the 1st
Kind of Boundary Condition. Small Time Forms. All evaluated at n' = L. Simpler and still
accurate equations are given if the functions of 2L + x and 3L - x are dropped.
| Number | Equation |
| 3B.X11 |
- |
|
+ K(L + x)(1 - (L + x)2(2 |
|
|
+ (1/2)K(3L - x)(1 - (3L - x)2(2 |
|
3B.X12 |
|
| + (L + x)K(L + x) - (1/2)(3L - x)K(3L - x)] | |
3B.X13 |
|
| - (1/2)(3L - x)K(3L - x)] - 2(h0/k)[K(L - x) + K(L + x) | |
| - K(3L - x)] + (h0/k)2[H0(L - x) + H0(L + x) - H0(3L - x)] | |
3B.X21 |
- |
|
- K(L + x)(1 - (L + x)2(2 |
|
|
- (1/2)K(3L - x)(1 - (3L - x)2(2 |
|
3B.X22 |
|
| - (L + x)K(L + x) + (1/2)(3L - x)K(3L - x)] | |
3B.X23 |
|
| + (1/2)(3L - x)K(3L - x)] - 2(hL/k)[K(L - x) - K(L + x) | |
| + K(3L - x)] + (hL/k)2[HL(L - x) - HL(L + x) + HL(3L - x)] | |
3B.X31 |
- |
|
- K(L + x)(1 - (L + x)2(2 |
|
|
- (1/2)K(3L - x)(1 - (3L - x)2(2 |
|
|
-4(h0/k)K(L + x)[(hL/k) - (L + x)(2 |
|
|
-2(hL/k)K(3L - x)[(hL/k) - (3L - x)(2 |
|
| +2(hL/k)3HL(L + x) + (hL/k)3HL(3L - x) | |
3B.X32 |
|
| + (1/2)(3L - x)K(3L - x)] + 2(h0/k)[2K(L + x) - K(3L - x)] | |
| - (h0/k)2[2H0(L + x) - H0(3L - x)] | |
3B.X33a |
|
| + (1/2)(3L - x)K(3L - x)] + 2(h0/k)[2K(L + x) - K(3L - x)] | |
| - (h0/k)2[2H0(L + x) - H0(3L - x)] - 2(hL/k)[K(L - x) | |
| - K(L + x) + K(3L - x)] + (hL/k)2[HL(L - x) - HL(L + x) | |
| + HL(3L - x)] + DJH(L, x, L) | |
| where for
h0 |
|
3B.X33b |
DJH(L, x, L) = (2h0hL/(k(hL - h0)))[(h0/k)(H0(L + x) |
| - H0(3L - x)) - (hL/k)(HL(L + x) - HL(3L - x)] | |
| and for h0 = hL, | |
3B.X33c |
DJH(L, x, L) = (2h02/k2){4(h0/k) |
|
- [1 + (h0/k)(L + x) + 2(h0/k)2 |
|
|
+ [1 + (h0/k)(3L - x) + 2(h0/k)2 |
Table 4A. Integrals of small time form of Green's functions, from
x' = 0 to L for the finite cases
and from x' = 0 to ![]() for the XI0 cases. The X10, X20, X22 and X30 results are exact.
Note that
erfc
(2/(4 . 0.05)1/2)
for the XI0 cases. The X10, X20, X22 and X30 results are exact.
Note that
erfc
(2/(4 . 0.05)1/2) ![]() 2.54E - 10 and erfc
(3/(4 . 0.05)1/2)
2.54E - 10 and erfc
(3/(4 . 0.05)1/2) ![]() 2.38E - 21
so for dimensionless times less
than 0.05 the E(2L + x) and E(3L - x) terms can be dropped. Note that we define
2.38E - 21
so for dimensionless times less
than 0.05 the E(2L + x) and E(3L - x) terms can be dropped. Note that we define
| Number | Equation |
| 4A.X10 |
|
4A.X11 |
|
| (1/2)[E(2L + x) + E(3L - x)] | |
4A.X12 |
|
| + E(3L - x)] | |
4A.X13 |
|
| + E(2L - x) + HL(L - x) - HL(L + x) - 2HL(2L - x) | |
| - (1/2)[E(2L + x) + E(3L - x)] + HL(2L + x) + HL(3L - x) | |
4A.X20 |
|
4A.X21 |
|
| + E(3L - x)] | |
4A.X22 |
|
4A.X23 |
|
| + HL(L - x) + HL(L + x) + (1/2)[E(2L + x) + E(3L - x)] | |
| - [HL(2L + x) + HL(3L - x)] | |
4A.X30 |
|
4A.X31 |
|
| + H0(x) - 2H0(L + x) - H0(2L - x) - (1/2)[E(2L + x) + E(3L - x)] + | |
| H0(2L + x) + H0(3L - x) | |
4A.X32 |
|
| + (1/2)[E(2L + x) + E(3L - x)] - [H0(2L + x) + H0(3L - x)] | |
4A.X33a |
|
| + H0(x) + H0(2L - x) + HL(L + x) + HL(L - x) + IJH(L, x) | |
| where for
h0 |
|
4A.X33b |
IJH(L, x) = 2E(L + x) + 2E(2L - x) - 2E(2L + x) - 2E(3L - x) |
| - (2hL/(hL - h0))[H0(2L - x) + H0(L + x) - H0(2L + x) | |
| - H0(3L - x)] + (2h0/(hL - h0))[HL(2L - x) + HL(L + x) | |
| - HL(2L + x) - HL(3L - x)] | |
| and where for h0 = hL = h, | |
4A.X33c |
IJH(L, x) = 2E(L + x) + 2E(2L - x) - 2E(2L + x) - 2E(3L - x) |
|
+2H0(2L - x)[- 1 + 2 |
|
|
+2H0(L + x))[- 1 + 2 |
|
|
-2H0(2L + x)[- 1 + 2 |
|
|
-2H0(3L - x)[- 1 + 2 |
|
|
- (8h |
Table 4B. Derivative wrt x of integrals of small time form of Green's functions,
from x' = 0 to L.
| Number | Equation |
4B.X11 |
|
| + K(2L - x)] + K(2L + x) - K(3L - x) | |
4B.X12 |
|
| - K(2L + x) + K(3L - x) | |
4B.X13 |
|
| + K(3L - x) - hL/k[HL(L - x) + HL(L + x) - 2HL(2L - x) | |
| - HL(2L + x) + HL(3L - x)] | |
4B.X21 |
|
| - K(2L + x) + K(3L - x) | |
4B.X22 |
|
4B.X23 |
|
| - hL/k[HL(L - x) - HL(L + x) + HL(2L + x) - HL(3L - x)] | |
4B.X31 |
|
| - K(2L + x) + K(3L - x) + h0/k[H0(x) - 2H0(L + x) | |
| + H0(2L - x) + H0(2L + x) - H0(3L - x)] | |
4B.X32 |
|
| + h0/k[H0(x) - H0(2L - x) - H0(2L + x) + H0(3L - x)] | |
4B.X33a |
|
| + h0/k[H0(x) - H0(2L - x) - H0(2L + x) + H0(3L - x)] | |
| - hL/k[HL(L - x) - HL(L + x) + HL(2L + x) - HL(3L - x)] + DIJH | |
| where for
h0 |
|
4B.X33b |
DIJH = 2h0hL/k(hL - h0)[- H0(L + x) + H0(2L - x) |
| + H0(2L + x) - H0(3L - x) + HL(L + x) - HL(2L - x) | |
| - HL(2L + x) + HL(3L - x)] | |
| and for h0 = hL = h, | |
4B.X33c |
DIJH = 2h2/k2{4 |
|
- K(3L - x)](L + x + 2h |
|
|
- (2L - x + 2h |
|
|
+ (3L - x + 2h |