| GX11(x, t | x |
= | [4 |
|
x 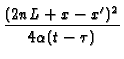
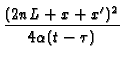
|
| GX11(x, t | x |
= | [4 |
|
x 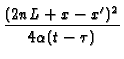
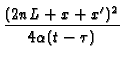
|
GX11(x, t | x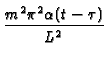
|
| GX12(x, t |
= | [4 |
|
x 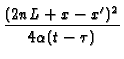
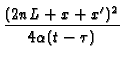
|
| GX12(x, t |
= | 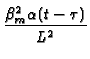
|
|
| where |
= | (2m - 1)( |
| GX13(x, t |
[4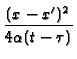
|
||
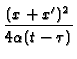
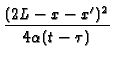
|
|||
- 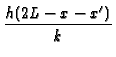 + h2
+ h2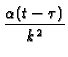
|
|||
x erfc![$\displaystyle {\frac{2L-x-x^{\prime }}{\left[ 4\alpha (t-\tau )%
\right] ^{1/2}}}$](img85.gif) + h
+ h![$\displaystyle {\frac{\left[ \alpha (t-\tau )\right] ^{1/2}}{k}}$](img86.gif)
|
| GX13(x, t |
= | 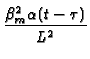
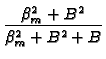
|
|
| x sin( |
|||
| with |
| GX14(x, t |
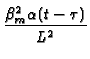
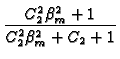
|
||
| x sin( |
|||
| with |
= | ||
| and where C2 | = | 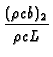 . . |
GX15(x, t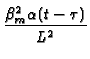
|
with Nm = 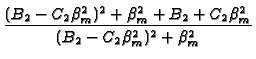 , , |
|||
| eigencondition (B2 - C2 |
|||
and where C2 = 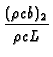 and B2 =
and B2 = |
| GX21(x, t |
= | [4 |
|
x 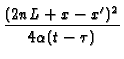
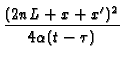
|
| GX21(x, t |
= | 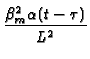
|
|
| where |
= | (2m - 1)( |
| GX22(x, t |
= | [4 |
|
x 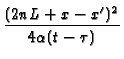
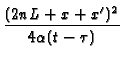
|
GX22(x, t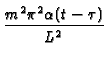
|
| GX23(x, t |
[4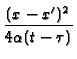
|
||
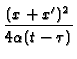
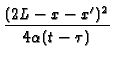
|
|||
- 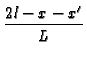 + B22
+ B22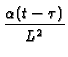
|
|||
x erfc![$\displaystyle {\frac{2L-x-x^{\prime }}{\left[ 4\alpha (t-\tau )
\right] ^{1/2}}}$](img126.gif) + B2
+ B2![$\displaystyle {\frac{\left[ \alpha (t-\tau )\right] ^{1/2}}{L}}$](img127.gif)
|
| GX23(x, t |
= | 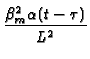
|
|
x 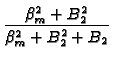
|
|||
| with |
= | B2 and where B2 = h2L/k. |
| GX24(x, t |
= | 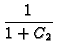 |
|
+ 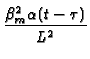
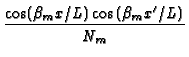 |
|||
| Nm | = | 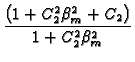 , , |
|
| with tan |
= | - C2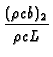 . . |
GX25(x, t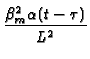
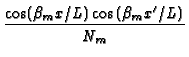 |
with Nm = ![$\displaystyle {\frac{\left[ \beta _{m}^{2}+D^{2}\right] (1+2C_{2})+D
\left[ 1-2C_{2}D\right] }{\beta _{m}^{2}+D^{2}}}$](img135.gif) , , |
|||
| eigencondition |
|||
and where B2 = 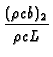 and D = (B2 - C2
and D = (B2 - C2 |
| GX31(x, t |
[4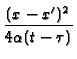
|
||
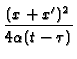
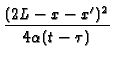
|
|||
- 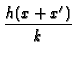 +
+ 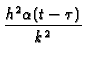
|
|||
x erfc![$\displaystyle {\frac{x+x^{\prime }}{\left[ 4\alpha (t-\tau )%
\right] ^{1/2}}}$](img141.gif) +
+ |
| GX31(x, t |
= | 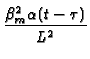
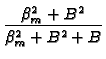
|
|
| x sin |
|||
| where |
= | - B and B = hL/k. |
| GX32(x, t |
[4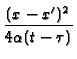
|
||
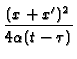
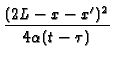
|
|||
- 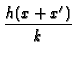 +
+ 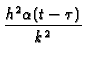
|
|||
x erfc![$\displaystyle {\frac{x+x^{\prime }}{\left[ 4\alpha (t-\tau )%
\right] ^{1/2}}}$](img141.gif) +
+ |
| GX32(x, t |
= | 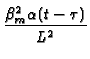
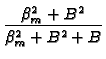
|
|
| x cos |
|||
| with |
= | B and where B = hL/k. |
| GX33(x, t |
[4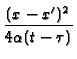
|
||
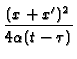
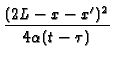
|
|||
- 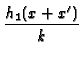 +
+ 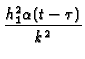
|
|||
x erfc![$\displaystyle {\frac{x+x^{\prime }}{\left[ 4\alpha (t-\tau )%
\right] ^{1/2}}}$](img141.gif) +
+ |
|||
- 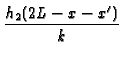 +
+ 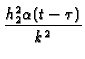
|
|||
x erfc![$\displaystyle {\frac{2L-x-x^{\prime }}{\left[ 4\alpha (t-\tau )%
\right] ^{1/2}}}$](img85.gif) +
+ |
| GX33(x, t |
= | 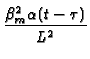
|
|
| x |
|||
x ![$\displaystyle {\frac{\left[ \beta _{m}\cos (\beta _{m}x^{\prime }/L)+B_{1}\sin
...
...ta _{m}^{2}+B_{1}^{2})\left[
1+B_{2}/(\beta _{m}^{2}+B_{2}^{2})\right] +B_{1}}}$](img165.gif) |
|||
| with tan |
= | 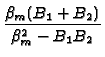 and where B1 =
and where B1 = |
| GX34(x, t |
= | 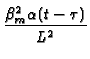
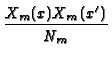 |
|
| where Xm(x) | = | B1sin( |
|
| Nm | = | 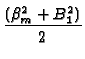 +
+ 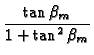
|
|
x 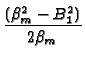 + 2C2B1
+ 2C2B1 |
|||
| with tan |
= | 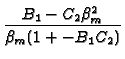 and where B1 =
and where B1 = 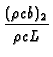 . . |
| GX35(x, t |
= | 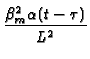
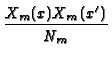 |
|
| where Xm(x) | = | B1sin( |
|
| Nm | = | 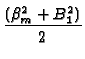 +
+ 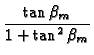 |
|
x 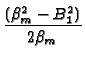 + 2C2B1
+ 2C2B1 |
|||
| with tan |
= | 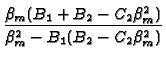 |
|
| and B1 | = | 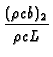 . . |
| GX41(x, t |
= | 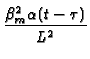
|
|
| x sin |
|||
| Nm = |
|||
| where |
= | 1/C1, C1 = 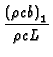 . . |
| GX42(x, t |
= | 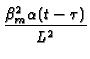
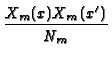
|
|
| where Xm(x) | = | cos( |
|
| N0 | = | 1 + C1, Nm = |
|
| where |
= | -1/C1, C1 = 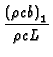 . . |
| GX51(x, t |
= | 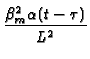
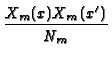 |
|
| where Xm(x) | = | Dmsin( |
|
| Nm | = | ||
| where tan |
= | 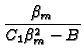 , C1 = , C1 = 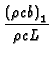 , B = , B = |
| GX52(x, t |
= | 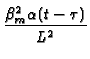
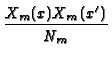 |
|
| where Xm(x) | = | Dmsin( |
|
| Nm | = | ||
| where tan |
= | Dm, C1 = 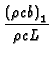 , B = , B = |