GX10(x, t | x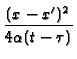
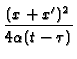
|
GX10(x, t | x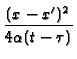
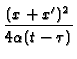
|
GX20(x, t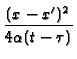
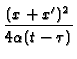
|
| GX30(x, t |
= | [4 |
|
x 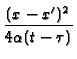
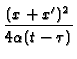
|
|||
| - |
|||
x erfc![$\displaystyle {\frac{x+x^{\prime }}{[4\alpha (t-\tau )]^{1/2}}}$](img28.gif) +
+ |
| GX40(x, t |
= | [4 |
|
x 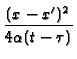
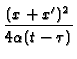
|
|||
+ 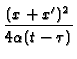
|
|||
x rerf![$\displaystyle {\frac{x+x^{\prime }}{[4\alpha (t-\tau )]^{1/2}}}$](img28.gif) +
+ ![$\displaystyle {\frac{[\alpha (t-\tau )]^{1/2}}{b}}$](img36.gif)
|
|||
| where P | = |
| GX50(x, t |
= | [4 |
|
x 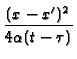
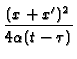
|
|||
+ 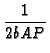 exp exp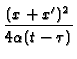
|
|||
x ![$\displaystyle {\frac{x+x^{\prime }}{[4\alpha (t-\tau )]^{1/2}}}$](img28.gif) + (1 + A)
+ (1 + A)![$\displaystyle {\frac{[\alpha (t-\tau )]^{1/2}}{2bP}}$](img42.gif)
|
|||
![$\displaystyle {\frac{x+x^{\prime }}{[4\alpha (t-\tau )]^{1/2}}}$](img28.gif) + (1 - A)
+ (1 - A)![$\displaystyle {\frac{[\alpha (t-\tau )]^{1/2}}{2bP}}$](img42.gif)
|
|||
| where P | = | ||
| rerf (z) | = | exp(z2)erfc(z) |