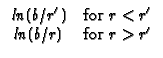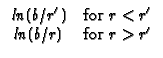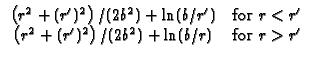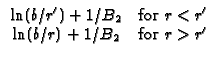

Next: Hollow Cylinder, steady 1-D.
Up: Radial-Cylindrical Coordinates. Steady 1-D.
Previous: Infinite body with a
R01 Solid cylinder,
0 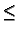 r
r 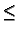 b, with G <
b, with G < 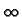 (natural boundary) at r = 0, and G = 0 (Dirichlet) at r = b.
R02 Solid cylinder,
0
(natural boundary) at r = 0, and G = 0 (Dirichlet) at r = b.
R02 Solid cylinder,
0 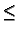 r
r 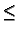 b, with G <
b, with G < 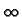 (natural boundary) at r = 0, and
(natural boundary) at r = 0, and
 G/
G/ r = 0 (Neumann) at r = b
. Note that this geometry requires a pseudo GF, denoted H. The
temperature solution found from a pseudo GF requires that the total
volumetric heat flow is equal to the boundary heat flow, and the spatial
average temperature in the body must be supplied as a known condition.
R03 Solid cylinder,
0
r = 0 (Neumann) at r = b
. Note that this geometry requires a pseudo GF, denoted H. The
temperature solution found from a pseudo GF requires that the total
volumetric heat flow is equal to the boundary heat flow, and the spatial
average temperature in the body must be supplied as a known condition.
R03 Solid cylinder,
0 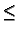 r
r 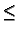 b, with G <
b, with G < 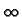 (natural boundary) at r = 0 and
k
(natural boundary) at r = 0 and
k G/
G/ r + h2G = 0
(convection) at r = b. Note
B2 = h2b/k.
r + h2G = 0
(convection) at r = b. Note
B2 = h2b/k.
Kevin D. Cole
2002-12-31