

Next: Radial Cylindrical Coordinates, Steady 2D and 3D. Cases R0JZKL and R0JZKL
Up: Radial-Cylindrical Coordinates. Steady 1-D.
Previous: Solid cylinder, steady 1-D.
and R0JZKL
Up: Radial-Cylindrical Coordinates. Steady 1-D.
Previous: Solid cylinder, steady 1-D.
R11 Hollow cylinder,
a  r
r  b, with G = 0
(Dirichlet) at r=a and at r=b.
R12 Hollow cylinder,
a
b, with G = 0
(Dirichlet) at r=a and at r=b.
R12 Hollow cylinder,
a  r
r  b, with G = 0
(Dirichlet) at r = a and
b, with G = 0
(Dirichlet) at r = a and
 G/
G/ r = 0 (Neumann) at r = b.
R13 Hollow cylinder,
0
r = 0 (Neumann) at r = b.
R13 Hollow cylinder,
0  r
r  b, with G = 0
(Dirichlet) at r = 0 and
k
b, with G = 0
(Dirichlet) at r = 0 and
k G/
G/ r + h2G = 0 (convection) at r = b. Note
B2 = h2b/k.
R21 Hollow cylinder,
a
r + h2G = 0 (convection) at r = b. Note
B2 = h2b/k.
R21 Hollow cylinder,
a  r
r  b, with
b, with
 G/
G/ r = 0 (Neumann) at r = a and G = 0 (Dirichlet) at r = b.
R22 Hollow cylinder,
a
r = 0 (Neumann) at r = a and G = 0 (Dirichlet) at r = b.
R22 Hollow cylinder,
a  r
r  b, with
b, with
 G/
G/ r = 0 (Neumann) at both boundaries. Note that this geometry
requires a pseudo GF, denoted H. The temperature solution found from a
pseudo GF requires that the total volumetric heat flow is equal to the
boundary heat flow, and the spatial average temperature in the body must be
supplied as a known condition.
R23 Hollow cylinder,
a
r = 0 (Neumann) at both boundaries. Note that this geometry
requires a pseudo GF, denoted H. The temperature solution found from a
pseudo GF requires that the total volumetric heat flow is equal to the
boundary heat flow, and the spatial average temperature in the body must be
supplied as a known condition.
R23 Hollow cylinder,
a  r
r  b, with
b, with
 G/
G/ r = 0 (Neumann) at r = a and
k
r = 0 (Neumann) at r = a and
k G/
G/ r + h2G = 0
(convection) at r = b. Note
B2 = h2b/k.
R31 Hollow cylinder,
a
r + h2G = 0
(convection) at r = b. Note
B2 = h2b/k.
R31 Hollow cylinder,
a  r
r  b, with
- k
b, with
- k G/
G/ r + h1G = 0 (convection) at r = a and G = 0 (Dirichlet) at r = b.
Note
B1 = h1a/k
R32 Hollow cylinder,
a
r + h1G = 0 (convection) at r = a and G = 0 (Dirichlet) at r = b.
Note
B1 = h1a/k
R32 Hollow cylinder,
a  r
r  b, with
- k
b, with
- k G/
G/ r + h2G = 0 (convection) at r = a and
r + h2G = 0 (convection) at r = a and
 G/
G/ r = 0
(Neumann) at r = b. Note
B1 = h1a/k.
R33 Hollow cylinder,
a
r = 0
(Neumann) at r = b. Note
B1 = h1a/k.
R33 Hollow cylinder,
a  r
r  b, with
- k
b, with
- k G/
G/ r + h1G = 0 (convection) at r = a and
k
r + h1G = 0 (convection) at r = a and
k G/
G/ r + h2G = 0 (convection) at r = b. Note
B1 = h1a/k and
B2 = h2b/k.
r + h2G = 0 (convection) at r = b. Note
B1 = h1a/k and
B2 = h2b/k.


Next: Radial Cylindrical Coordinates, Steady 2D and 3D. Cases R0JZKL and R0JZKL
Up: Radial-Cylindrical Coordinates. Steady 1-D.
Previous: Solid cylinder, steady 1-D.
Kevin D. Cole
and R0JZKL
Up: Radial-Cylindrical Coordinates. Steady 1-D.
Previous: Solid cylinder, steady 1-D.
Kevin D. Cole
2002-12-31
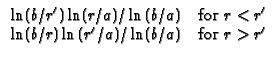
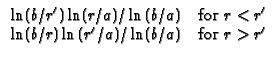
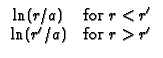
![$\displaystyle \begin{array}{cc}
\ln (r/a)\left[ 1+B_{2}\ln (b/r^{\prime })\rig...
...[1+B_{2}\ln (b/r)]/[1+B_{2}\ln (b/a)] & \text{for }
r>r^{\prime }
\end{array}$](img558.gif)
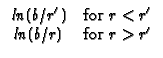
![$\displaystyle \begin{array}{c}
\lbrack (r^{2}+(r^{\prime })^{2})/2-b^{2}\ln (\...
...ac{%
r^{\prime }}{a})]/(b^{2}-a^{2}) \\
\text{for }r>r^{\prime }
\end{array}$](img561.gif)
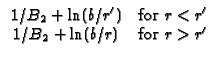
![$\displaystyle \begin{array}{cc}
\ln (b/r^{\prime })[1+B_{1}\ln (r/a)]/[1+B_{1}...
...n (r^{\prime }/a)]/[1+B_{1}\ln (b/a)] & \text{for }%
r>r^{\prime }
\end{array}$](img567.gif)
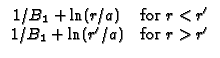
![$\displaystyle \begin{array}{c}
\lbrack B_{1}B_{2}ln(b/r^{\prime })ln(r/a)+B_{1...
... \lbrack B_{1}+B_{2}+B_{1}B_{2}ln(b/a)];\;\text{for }r>r^{\prime }
\end{array}$](img573.gif)