Representations of $\delta (x)$.

In use, the Dirac delta function is never evaluated without multiplying by a test function and integrating over some domain. Equations involving Dirac delta functions without such integrations are a convenient half-way stage that nevertheless have enormous utility. Properly speaking, the Dirac delta function is not a function at all (it is a generalized function or a functional), however it can be represented as the limit of a sequence of ordinary functions.

Representations of the Dirac delta with familiar functions allow us to visualize the Dirac delta, and many calculations involving $\delta (x)$ can be carried out with these representations. Let $F(x,\epsilon )$ be a function that has a peak near $x=0$, and the shape of the peak is controlled by parameter $\epsilon$. If the integral of $F(x,\epsilon )$ is unity, that is,

$$\int_{-\infty }^{\infty }F(x,\epsilon )\,dx=1$$

for any value of parameter $\epsilon >0$, then the Dirac delta function may be represented in the limit:

$$\delta (x)=\lim_{\epsilon \rightarrow 0}\;F(x,\epsilon )$$

Example representations:

1. Top-hat function (square step).
   
   $$F(x,\epsilon )=\left\{ \begin{array}{cc} 1/\epsilon & -\eps... ... /2<x<\epsilon /2 \\ 0 & \mbox{otherwise} \end{array}\right.$$
   
   

2. Diffraction peak.
   
   $$F(x,\epsilon )=\frac{\sin (x/\epsilon )}{\pi x}$$
   
   

3. Lorentzian.
   
   $$F(x,\epsilon )=\frac{\epsilon /\pi }{(x^{2}+\epsilon ^{2})}$$
   
   

4. Gaussian.
   
   $$F(x,\epsilon )=\frac{1}{2\epsilon }\exp (-x^{2}/\epsilon ^{2})$$
   
   

5. Fourier integral. Using a standard integral, the Lorentz representation may be written
   
   $$F(x,\epsilon )=\frac{\epsilon /\pi }{(x^{2}+\epsilon ^{2})}=... ...\infty }\exp (-\epsilon \left\vert k\right\vert )\cos (kx)\;dk$$
   
   
   and the limit can be explicitly evaluated to obtain
   
   $$\lim_{\epsilon \rightarrow 0}F(x,\epsilon )=\delta (x)=\frac{1}{2\pi }% \int_{-\infty }^{\infty }\exp (ikx)\;dk$$
   
   

Figure: Representations of the Dirac delta function.

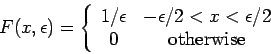
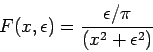
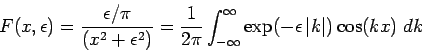
NOTE: Although all of the above functions $F(x,\epsilon )$ are symmetric, symmetry is not essential. Non-symmetric functions produce perfectly good representations of the Dirac delta function.