

Next: Dirac delta function
Up: What is Green's Function
Previous: Another Interpretation of G
The following properties are common to Green's functions for the heat
equation on domain  .
.
- Auxiliary problem.
 Every GF satisfies an auxiliary problem, which
includes a Dirac delta generation term in the differential equation, homogeneous boundary conditions of the same type as the original boundary
value problem, and a homogeneous initial condition.
Every GF satisfies an auxiliary problem, which
includes a Dirac delta generation term in the differential equation, homogeneous boundary conditions of the same type as the original boundary
value problem, and a homogeneous initial condition.
- Causality.
 In domain
In domain  ,
, 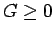 for
for  , and
, and 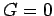 for
for 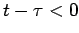 . This is called the causality relation, because the GF
exhibits zero response until after the heat impulse appears.
. This is called the causality relation, because the GF
exhibits zero response until after the heat impulse appears.
- Reciprocity.
 . This follows from the heat
equation which is second order in space and first order in time.
. This follows from the heat
equation which is second order in space and first order in time.
- Time dependence. The time dependence of
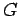 is always
is always 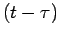 ,
so the functional form of a one-dimensional GF could be written
,
so the functional form of a one-dimensional GF could be written
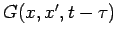 .
.
- Units. The transient GF takes its units from the (spatial) Dirac delta
function, which depends on the dimensionality of the problem. For the heat
equation in rectangular coordinates,
![$\left[ G\right] =m^{-1}$](img58.png) for
one-dimensional problems,
for
one-dimensional problems,
![$\left[ G\right] =m^{-2}$](img59.png) for two-dimensional
problems, and
for two-dimensional
problems, and
![$\left[ G\right] =m^{-3}$](img60.png) for three-dimensional problems.
for three-dimensional problems.


Next: Dirac delta function
Up: What is Green's Function
Previous: Another Interpretation of G
2004-01-21
![]() .
.