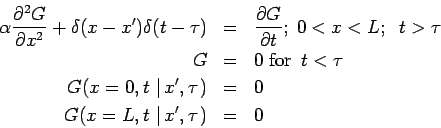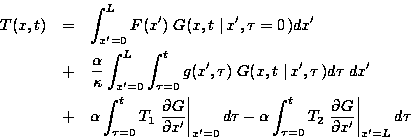

Next: Another Interpretation of G
Up: What is Green's Function
Previous: FIN EQUATION EXAMPLE
The heat equation descibes transient heat conduction in solids. Consider the
following boundary value problem for the temperature in a one-dimensional
plate:
Here we seek the temperature 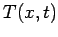 (units: Kelvin) in a one-dimensional
plate
(units: Kelvin) in a one-dimensional
plate 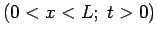 caused by a specified energy generation function
caused by a specified energy generation function 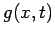 (units: Watts/m
(units: Watts/m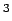 ) inside the body. Initially the temperature
is a known function
) inside the body. Initially the temperature
is a known function 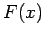 . Refer to the figure for the geometry.
. Refer to the figure for the geometry.
Figure:
Geometry for transient one-dimensional example.
![\includegraphics[height=4cm]{whatisG_1Dexample.eps}](img32.png) |
The thermal properties are conductivity  (
(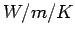 ) and diffusivity
) and diffusivity 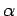
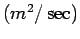 . Since
this is a second order equation two boundary conditions are needed, and in
this example at each boundary the temperature is specified (Dirichlet, or
type 1, boundary conditions). Other types of boundary conditions are
possible.
. Since
this is a second order equation two boundary conditions are needed, and in
this example at each boundary the temperature is specified (Dirichlet, or
type 1, boundary conditions). Other types of boundary conditions are
possible.
The temperature that satisifies the above equations will be found in
two steps. First the GF will be defined, and then the GF will be used
to construct the temperature.
The Green's function
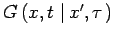 associated with the above example obeys the following equations:
associated with the above example obeys the following equations:
Note that the boundary conditions are of the same type as the temperature
problem, but homogeneous,
and that the energy generation term has been replaced by a
product of two Dirac delta functions
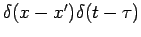 , one for space and one for time. The units of
, one for space and one for time. The units of 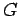 are determined by the
units of the Dirac delta function, and in this 1-D Cartesian case
are determined by the
units of the Dirac delta function, and in this 1-D Cartesian case
![$\left[ G\right] =meters^{-1}$](img40.png) . The Green's function
. The Green's function
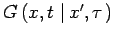 represents
the temperature response observed at point
represents
the temperature response observed at point 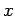 and time
and time 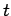 caused by an
instantaneous concentrated heat source released at point
caused by an
instantaneous concentrated heat source released at point 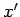 and
time
and
time 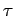 . Green's functions are causal since there is no response
before the heat source is released:
. Green's functions are causal since there is no response
before the heat source is released: 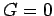 for
for 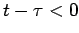 .
Finally, the thermal properties
are constant so the differential equation is linear; this is important since
the Green's functions may only be found for linear differential equations.
.
Finally, the thermal properties
are constant so the differential equation is linear; this is important since
the Green's functions may only be found for linear differential equations.
The temperature solution is constructed from a suitable distribution of
the GF within the body so as to reproduce the heating conditions. The
temperature for this example is given by:
In this temperature expression there is a separate additive term
associated with each non-zero
heating term: the initial condition; the energy generation; and,
one term for each boundary. See ``GF Solution Equation'' for a general
discussion of transient temperature described by the GF method.


Next: Another Interpretation of G
Up: What is Green's Function
Previous: FIN EQUATION EXAMPLE
2004-01-21
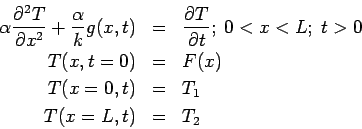
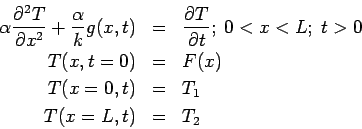
![]() associated with the above example obeys the following equations:
associated with the above example obeys the following equations: