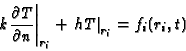
Here h is the heat transfer coefficient and
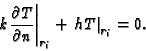
Here T is temperature, k is conductivity, g is energy generation,
qsurface=h(Tsurface-Tfluid) .
When m2 is real this equation describes steady heat with ``side'' heat losses (fin losses). When m2 is imaginary the Helmholtz equation is the heat equation in Fourier-transform space (also called the thermal-wave equation). Finally, replace -m2 by real +m2 to give the wave equation in Fourier-transform space.
type 1, T = 0;
type 2,
type 3,
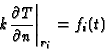
where