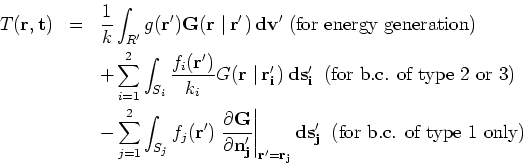

Next: EXAMPLES, TEMPERATURE FROM GF
Up: Laplace and Helmholtz Equation
Previous: Steady, 1-D Body, Rectangular
Consider steady heat transfer in any orthogonal coordinate system:
where
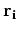 is located on surface
is located on surface 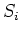 . The boundary
condition is type 3; heat transfer coefficient
. The boundary
condition is type 3; heat transfer coefficient 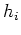 can vary with
position on surface
can vary with
position on surface 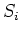 but is independent of temperature. Boundary
conditions of type 1 and 2 may be obtained from the above boundary condition
can be obtained by setting
but is independent of temperature. Boundary
conditions of type 1 and 2 may be obtained from the above boundary condition
can be obtained by setting 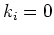 or
or  , respectively.
, respectively.
The Green's function solution equation for steady temperature 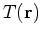 is given by:
is given by:
See Table 1 (under Heat Equation, General Case) for 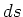 and
and 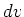 for
various geometries in rectangular, cylindrical, and spherical coordinates.
for
various geometries in rectangular, cylindrical, and spherical coordinates.
2004-01-31
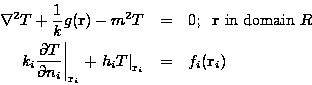
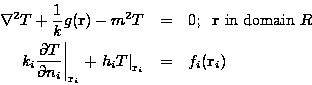
![]() is given by:
is given by: