Steady, 1-D Body, Rectangular Coordinates

Consider steady heat conduction in a one-dimensional body, rectangular coordinates:

$$\begin{eqnarray*} \frac{\partial ^{2}T}{\partial x^{2}}+\frac{1}{k}g(x)-m^{2}T &... ...n_{i}}\right\vert _{x_{i}}+h_{i}T(x_{i}) &=& f_{i}; \; \; i=1,2. \end{eqnarray*}$$

The 1-D rectangular Green's function solution equation for the steady temperature 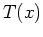$T(x)$ is given by:

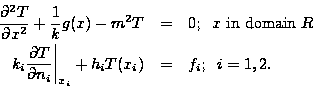
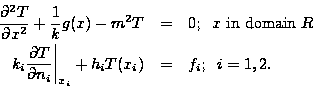
$$\begin{eqnarray*} T(x,t) &=&\frac{1}{k}\int_{x^{\prime }}g(x^{\prime })G(x \lef... ... _{x^{\prime }=x_{i}}\right] \; \mbox{(for b.c. of type 1 only)} \end{eqnarray*}$$