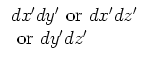

Next: Laplace and Helmholtz Equation
Up: HEAT EQUATION (TRANSIENT CONDUCTION)
Previous: Heat Equation, 1-D Rectangular
Consider the following general boundary-value problem with vector coordinate
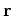 :
:
The general boundary condition represents five different boundary conditions
(type 1
through 5) by suitable choice of boundary parameters 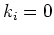 or
or 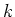 ;
; 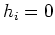 or
or 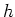 ;
;
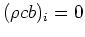 or nonzero.
or nonzero.  Here
Here 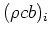 represents properties of a high conductivity surface film (density, specific
heat, thickness) which is thin enough that there is a negligible temperature
gradient across the film and negligible heat flux parallel to the surface
inside the film.
represents properties of a high conductivity surface film (density, specific
heat, thickness) which is thin enough that there is a negligible temperature
gradient across the film and negligible heat flux parallel to the surface
inside the film.
The Green's Function Solution Equation for temperature
 is
given by:
is
given by:
This equation applies to any orthogonal coordinate system if the correct
form for differential area 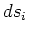 and differential volume
and differential volume 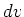 are used. See the table below for
are used. See the table below for 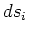 and
and 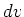 for several body shapes in the
rectangular, cylindrical, and spherical coordinate systems. Spatial
derivative
for several body shapes in the
rectangular, cylindrical, and spherical coordinate systems. Spatial
derivative
 denotes differentiation along the
outward normal on surface
denotes differentiation along the
outward normal on surface 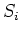 ,
,
 where
where 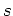 represents the number of boundary conditions. The number of boundary
conditions
represents the number of boundary conditions. The number of boundary
conditions 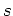 only includes conditions at ``real'' boundaries; the number
of ``real'' boundaries does not include the boundary at
only includes conditions at ``real'' boundaries; the number
of ``real'' boundaries does not include the boundary at
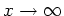 for a semi-infinite body, for example.
for a semi-infinite body, for example.
Table 1. Differential area and volume for the GF Solution Equation.
| Body shape |
coordinates |
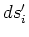 |
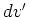 |
| plate |
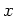 |
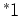 |
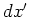 |
| rectangle |
 |
 |
 |
| parallelpiped |
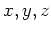 |
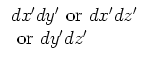 |
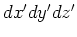 |
| infinite cylinder |
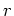 |
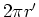 |
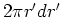 |
| thin shell |
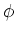 |
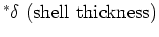 |
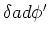 |
| finite cylinder |
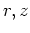 |
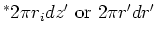 |
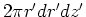 |
| wedge |
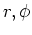 |
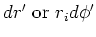 |
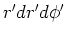 |
| sphere |
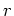 |
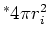 |
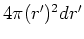 |
 |
|
|
|


Next: Laplace and Helmholtz Equation
Up: HEAT EQUATION (TRANSIENT CONDUCTION)
Previous: Heat Equation, 1-D Rectangular
2004-01-31
![]() :
:
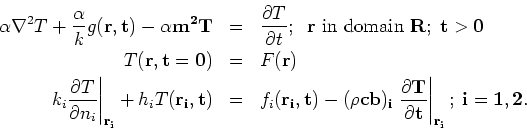
![]() is
given by:
is
given by:
![\begin{eqnarray*}
&&T(\mathbf{r},t)=\int_{R}G(\mathbf{r},t \left\vert \mathbf...
...{r}_{i}}\right] ds_{j}^{\prime } \;
\mbox{(b.c. of type 1 only)}
\end{eqnarray*}](img24.png)