

Next: Heat Equation, General Case
Up: HEAT EQUATION (TRANSIENT CONDUCTION)
Previous: HEAT EQUATION (TRANSIENT CONDUCTION)
Consider the following boundary-value problem for temperature in a 1-D body
in rectangular coordinates:
Note that 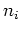 is the outward normal on boundary
is the outward normal on boundary 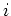 . The convective
(type 3) boundary conditions are specified on boundaries
. The convective
(type 3) boundary conditions are specified on boundaries 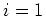 and
and 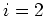 . Boundary conditions of type 1 or 2 are also included by this relationship by
taking
. Boundary conditions of type 1 or 2 are also included by this relationship by
taking 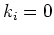 or
or  , respectively, on boundaries
, respectively, on boundaries 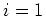 or
or 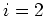 .
.
The Green's Function Solution Equation for temperature 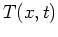 is given by:
is given by:
The spatial integrals should be evaluated over the whole body, for example,
on
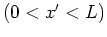 for a plate, or over
for a plate, or over
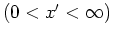 for a
semi-infinte body. The sumations in the boundary condition terms represent
at most two boundaries.
for a
semi-infinte body. The sumations in the boundary condition terms represent
at most two boundaries.
The same GF appears in each integral term, evaluated at the source location
 appropriate for that integral term. For example, in
the initial-condition integral the GF is evaluated at
appropriate for that integral term. For example, in
the initial-condition integral the GF is evaluated at 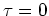 ; in a
boundary-condition integral the GF is evaluated at
; in a
boundary-condition integral the GF is evaluated at
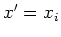 ,
,
2004-01-31
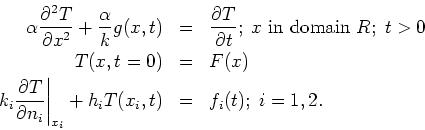
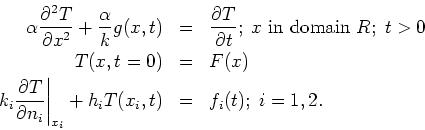
![]() is given by:
is given by:
![\begin{eqnarray*}
T(x,t) &=&\int_{x^{\prime }}G(x,t \left\vert x^{\prime },0\...
...{x^{\prime }=x_{i}}%
\right] \; \mbox{(for b.c. of type 1 only)}
\end{eqnarray*}](img9.png)
![]() appropriate for that integral term. For example, in
the initial-condition integral the GF is evaluated at
appropriate for that integral term. For example, in
the initial-condition integral the GF is evaluated at ![]() ; in a
boundary-condition integral the GF is evaluated at
; in a
boundary-condition integral the GF is evaluated at
![]() ,
,