

Next: About this document ...
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: Solid sphere with convection.
Consider the steady temperature in a rectangle caused by
heating on one face. Of the other faces, two are at zero
temperature and one is insulated. The temperature satisfies
the following equations:
This is case (X21B00)(Y21B10). The GF solution has the form:
 |
(32) |
There are three forms of the steady GF for the rectangle, a double-sum
expression (usually to be avoided) and two single-sum expressions.
Both single-sum forms of the GF form produce convergent temperature
expressions, but the speed of convergence varies through the rectangle.
In this example one form of the GF will be discussed,
that with kernel functions along the x-axis:
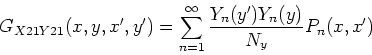 |
(33) |
The eigenfunction is
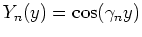 , the eigenvalues are
, the eigenvalues are
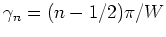 and the norm is
and the norm is 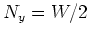 .
The kernel function is given by
.
The kernel function is given by
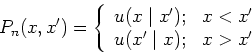 |
(34) |
where
Replace the GF into the temperature expression, and carry out the
integral to find
![\begin{displaymath}
T(x,y) = \frac{2 q_0 W}{k} \sum_{n=1}^{\infty}
\frac{\cos(\...
...ma_n (L-x)}+e^{-\gamma_n (L+x)} }
{1+e^{-2\gamma_n L}} \right]
\end{displaymath}](img191.png) |
(35) |
A full discussion of the above integral and numerical values
for the temperature are given in a paper
``Green's Functions, Temperature and Heat Flux in the Rectangle'' by
Kevin D. Cole and David H. Yen, accepted November 2000 for the International
Journal of Heat and Mass Transfer.


Next: About this document ...
Up: EXAMPLES, TEMPERATURE FROM GF
Previous: Solid sphere with convection.
2004-01-31

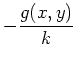
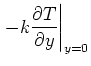
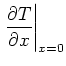

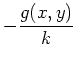
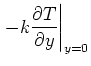
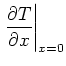
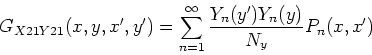
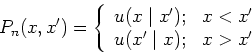
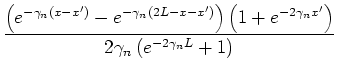
![\begin{displaymath}
T(x,y) = \frac{2 q_0 W}{k} \sum_{n=1}^{\infty}
\frac{\cos(\...
...ma_n (L-x)}+e^{-\gamma_n (L+x)} }
{1+e^{-2\gamma_n L}} \right]
\end{displaymath}](img191.png)