

Next: Rectangular Coordinates. Finite Bodies,
Up: Rectangular Coordinates. Steady 1-D.
Previous: Semi infinite body, steady
X11 Plate, G = 0 (Dirichlet) at x = 0 and x = L.
X12 Plate, G = 0 (Dirichlet) at x = 0 and
 G/
G/ x = 0 (Neumann) at x = L.
x = 0 (Neumann) at x = L.
X13 Plate, G = 0 (Dirichlet) at x = 0 and
k G/
G/ x + h2G = 0 (Neumann) at x = L Note
B2 = h2L/k
x + h2G = 0 (Neumann) at x = L Note
B2 = h2L/k
X21 Plate,
 G/
G/ x = 0 (Neumann) at x = 0
and G = 0 (Dirichlet) at x = L.
x = 0 (Neumann) at x = 0
and G = 0 (Dirichlet) at x = L.
X22 Plate,
 G/
G/ x = 0 (Neumann) at both
sides. Note that this geometry requires a pseudo GF, denoted H. The
temperature solution found from a pseudo GF requires that the total
volumetric heating sums to zero and the spatial average temperature in the
body must be supplied as a known condition.
x = 0 (Neumann) at both
sides. Note that this geometry requires a pseudo GF, denoted H. The
temperature solution found from a pseudo GF requires that the total
volumetric heating sums to zero and the spatial average temperature in the
body must be supplied as a known condition.
X23 Plate,
 G/
G/ x = 0 (Neumann) at x = 0
and
k
x = 0 (Neumann) at x = 0
and
k G/
G/ x + h2G = 0 (convection) at x = L. Note
B2 = h2L/k
x + h2G = 0 (convection) at x = L. Note
B2 = h2L/k
X31 Plate,
- k G/
G/ x + h1G = 0
(convection) at x = 0 and G = 0 (Dirchlet) at x = L. Note
B1 = h1L/k
x + h1G = 0
(convection) at x = 0 and G = 0 (Dirchlet) at x = L. Note
B1 = h1L/k
X32 Plate,
- k G/
G/ x + h1G = 0
(convection) at x = 0 and
x + h1G = 0
(convection) at x = 0 and
 G/
G/ x = 0 (Neumann) at x = L.
Note
B1 = h1L/k
x = 0 (Neumann) at x = L.
Note
B1 = h1L/k
X33 Plate,
- k G/
G/ x + h1G = 0
(convection) at x = 0 and
k
x + h1G = 0
(convection) at x = 0 and
k G/
G/ x + h2G = 0 (convection) at x = L. Note
B1 = h1L/k and
B2 = h2L/k
x + h2G = 0 (convection) at x = L. Note
B1 = h1L/k and
B2 = h2L/k
GX33(x 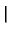 x x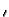  ) ) |
= |
 ; forx < x ; forx < x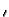 |
|
| |
= |
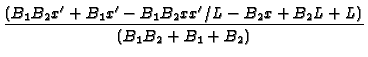 ; forx > x ; forx > x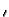 |
|


Next: Rectangular Coordinates. Finite Bodies,
Up: Rectangular Coordinates. Steady 1-D.
Previous: Semi infinite body, steady
Kevin D. Cole
2002-12-31
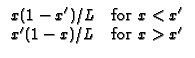
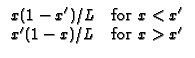
![]() G/
G/![]() x = 0 (Neumann) at x = L.
x = 0 (Neumann) at x = L.
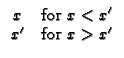
![]() G/
G/![]() x + h2G = 0 (Neumann) at x = L Note
B2 = h2L/k
x + h2G = 0 (Neumann) at x = L Note
B2 = h2L/k
![$\displaystyle \begin{array}{cc}
x[1-B_{2}(x^{\prime }/L)/(1+B_{2})] & \text{for...
... \\
x^{\prime }[1-B_{2}(x/L)/(1+B_{2})] & \text{for }x>x^{\prime }
\end{array}$](img430.gif)
![]() G/
G/![]() x = 0 (Neumann) at x = 0
and G = 0 (Dirichlet) at x = L.
x = 0 (Neumann) at x = 0
and G = 0 (Dirichlet) at x = L.
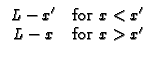
![$\displaystyle \begin{array}{cc}
\lbrack x^{2}+(x^{\prime })^{2}]/(2L)-x^{\prime...
...
\lbrack x^{2}+(x^{\prime })^{2}]/(2L)-x & \text{for }x>x^{\prime }
\end{array}$](img436.gif)
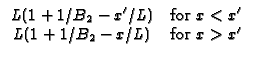
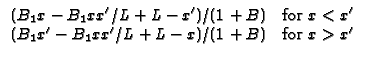

 ; forx < x
; forx < x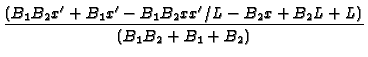 ; forx > x
; forx > x