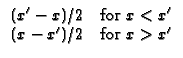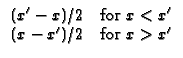

Next: Semi infinite body, steady
Up: Rectangular Coordinates. Steady 1-D.
Previous: Rectangular Coordinates. Steady 1-D.
X00 Infinite body,
- 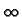 < x <
< x < 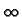 . Note that this
geometry requires a pseudo GF, denoted H. The temperature solution found
from a pseudo GF requires that the total volumetric heating sums to zero and
the spatial average temperature in the body must be supplied as a known
condition.
. Note that this
geometry requires a pseudo GF, denoted H. The temperature solution found
from a pseudo GF requires that the total volumetric heating sums to zero and
the spatial average temperature in the body must be supplied as a known
condition.
Kevin D. Cole
2002-12-31