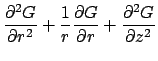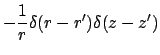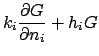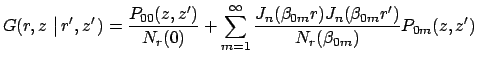

Next: Radial-spherical coordinates. Steady 1-D Radial.
Up: Radial Cylendrical Coordinates, Steady
Previous: GF, Double-Sum Form
Consider two-dimensional heat conduction in the finite cylinder.
The temperature is given by
The temperature may be stated in the form of integrals with
the method of Green's functions. If the Green's function, 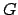 ,
is known, the temperature is given by
,
is known, the temperature is given by
(for volume energy generation)
(for boundary conditions of type 2 and 3)
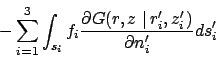 |
(13) |
(for boundary conditions of type 1 only).
The same Green's function appears in each integral but is evaluated at
locations appropriate for each integral. Here position
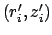 is located on
surface
is located on
surface 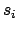 . Surface differential
. Surface differential 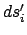 is associated with
appropriate surfaces of the cylinder: on surface
is associated with
appropriate surfaces of the cylinder: on surface 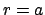 ,
,
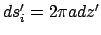 ; and, at
; and, at 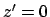 or
or 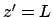 ,
,
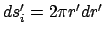 .
.
GF, 2D Cylinder
The steady Green's function represents the response at point 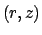 caused
by a point source of heat located at
caused
by a point source of heat located at
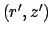 .
The GF for the finite cylinder satisfies the following equations:
.
The GF for the finite cylinder satisfies the following equations:
Note that the boundary conditions are homogeneous and of the same type
as the temperature problem.
The Green's function for the cylinder with axisymmetric heat conduction
is given by
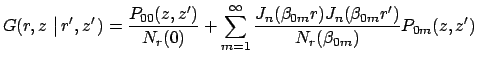 |
|
|
(15) |
| |
|
|
|
where 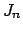 are Bessel functions of order
are Bessel functions of order 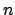 .
The norms, eigenconditions, and kernel functions are identical to those
used for the three-dimensional GF.
The above single-sum GF may be derived either by a direct solution
of the defining equation for
.
The norms, eigenconditions, and kernel functions are identical to those
used for the three-dimensional GF.
The above single-sum GF may be derived either by a direct solution
of the defining equation for  , or, by integrating the 3D GF
over
, or, by integrating the 3D GF
over
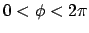 . A physical interpretation of this approach,
called the method of descent, is to distribute 3D point sources to
form a ring-shaped source appropriate for axisymmetric 2D heating.
A double-sum form of the GF may also be
found from the transient GF by the limit method; see Beck et al.
(1992, p. 249) for a discussion of case R01Z11.
. A physical interpretation of this approach,
called the method of descent, is to distribute 3D point sources to
form a ring-shaped source appropriate for axisymmetric 2D heating.
A double-sum form of the GF may also be
found from the transient GF by the limit method; see Beck et al.
(1992, p. 249) for a discussion of case R01Z11.


Next: Radial-spherical coordinates. Steady 1-D Radial.
Up: Radial Cylendrical Coordinates, Steady
Previous: GF, Double-Sum Form
Frank Pribyl
2005-06-07
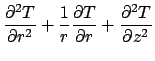
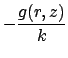
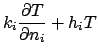
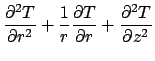
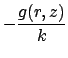
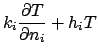
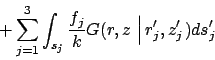
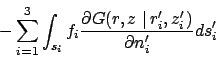
![]() caused
by a point source of heat located at
caused
by a point source of heat located at
![]() .
The GF for the finite cylinder satisfies the following equations:
.
The GF for the finite cylinder satisfies the following equations: